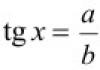Метод операционного исчисления. Как решить дифференциальное уравнение методом операционного исчисления

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ - совокупность методов прикладного математического анализа, позволяющих экономными и непосредственно ведущими к цели средствами получать решения линейных дифференциальных уравнений, а также разностных и некоторых типов интегральных уравнений. В связи с этим методы операционного исчисления находят самое широкое применение в механике, электротехнике, автоматике и в других самых разнообразных отраслях науки и техники. В основе операционного исчисления лежит идея функционального преобразования: некоторой функции вещественного переменного t, определенной при положительных значениях аргумента, называемой начальной функцией или оригиналом, с помощью линейного интегрального преобразования ставится в соответствие функция другого переменного р, называемая изображением. Подобное преобразование «оригинал - изображение» можно осуществить так, чтобы операциям дифференцирования и интегрирования начальных функций соответствовали алгебраические операции в области изображений. Это дает возможность находить с помощью простейших алгебраических действий изображения решений исходных дифференциальных уравнений, затем разыскивать соответствующую начальную функцию, т. е. решение осуществляется с помощью некоторых простых правил и «каталога» наиболее часто встречающихся изображений. В более сложных задачах приходится прибегать к обратному функциональному преобразованию: изображение - оригинал. Первые сочинения, посвященные операционному исчислению, появились в середине прошлого века. Русским математиком М. Е. Ващенко-Захарченко в монографии «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений», вышедшей в Киеве в 1862 г., были поставлены и частично разрешены основные задачи того метода, который в дальнейшем получил название операционного. Систематическое применение операционного исчисления к решению физических и технических задач началось с появления в 1892 г. работ английского ученого О. Хевисайда. Сущность операционного исчисления можно проиллюстрировать на примере с наиболее часто встречающимся в прикладных задачах классом начальных кусочно-непрерывных функций f(t) вещественной переменной t, определенных при tt<0. Из класса кусочно-непрерывных начальных функций выделяется и в дальнейшем рассматривается подкласс функций, характеризуемых определенным порядком роста при весьма больших значениях аргумента t, а именно: |f(t)| < Ме s o t , где М и s o - независимые от t числа. Если р=s+iσ - некоторое комплексное число, то при указанных ограничениях, накладываемых на функцию f(t), интеграл

существует и представляет регулярную в полуплоскости Rе р>s o функцию от р, называемую лапласовым интегралом функции f (t).
Функцию F (p), введенную по закону:

называют изображением начальной функции или оригинала f(t). Ряд свойств изображения (**), например изображения производной f’ (t):

и изображения интеграла

делают очевидным тот факт, что преобразование (*) переводит операции дифференцирования и интегрирования в операции умножения и деления на комплексное переменное р. Пользуясь основными свойствами изображения, составляются изображения некоторых простейших функций - «каталог» изображений. «Каталог» изображений простейших функций и теоремы разложения Хевисайда, дающие возможность отыскать начальную функцию, когда изображение F (р) является полиномом или отношением двух полиномов, позволяют простейшим способом найти решение большой группы обыкновенных линейных дифференциальных и разностных уравнений с постоянными коэффициентами. Но многочисленные задачи приводят к изображениям, не сводящимся к имеющимся в «каталоге». Существует общее средство построения начальной функции по ее изображению - так называемая формула обращения Римана-Меллина.

Лекция 2.

Применение операционного исчисления к решению линейных дифференциальных уравнений и систем уравнений с постоянными коэффициентами

Пусть требуется найти частное решение линейного дифференциального уравнения с постоянными коэффициентами

удовлетворяющее начальным условиям

где
- заданные числа.

Будем считать, что искомая функция
вместе с ее производными до– го порядка и функция
являются оригиналами.

Обозначим:
и
. Пользуясь свойством дифференцирования оригинала и свойством линейности, перейдем в дифференциальном уравнении от оригиналов к изображениям:

Полученное алгебраическое уравнение, линейное относительно изображения, называют операторным (или уравнением в изображениях). По найденному из него изображению
, можно найти оригинал
, используя таблицу и свойства преобразования Лапласа.

Пример 1. Операционным методом решить задачу Коши

,
,
.

Решение. Пусть
. Тогда ,

По таблице оригиналов и изображений

Подставляя эти выражения в дифференциальное уравнение, получаем операторное уравнение:

Разрешим его относительно
, получим

Найдем оригинал для каждого слагаемого в правой части полученного равенства.

Дробь
нужно представить в виде суммы простейших дробей.

Рациональная дробь
называется правильной, если степень
многочлена
меньше степенимногочлена
,т.е.
. Если дробь неправильная, то можно разделить числитель на знаменатель и выделить многочлен и правильную дробь. Простейшими дробями называются правильные рациональные дроби вида

;
;

.

Условие
означает, что многочлен
имеет комплексные корни.

Любую правильную рациональную дробь можно представить в виде суммы простейших дробей .

Если знаменатель представлен в виде разложения

где и- кратности соответствующих вещественных и комплексных корней, то разложение правильной рациональной дроби на простейшие будет иметь вид

(5)

Коэффициенты разложения
находят методом частных значений или методом неопределенных коэффициентов.

Дробь
представим в виде суммы простейших дробей

Умножив обе части последнего равенства на
, получим

Чтобы найти неопределенный коэффициент , подставим в это уравнение
. Тогда
, или
.

Приравнивая коэффициенты при ,ив обеих частях тождества, получим систему линейных уравнений

из которой можно найти остальные неопределенные коэффициенты и. Из первого уравнения этой системы
, из второго уравнения
. Следовательно,

Таким образом,

Пример 2. Операционным методом решить систему дифференциальных уравнений с заданными начальными условиями

,
,
.

Пусть
.Тогда
.

Так как
, то система операторных уравнений примет вид
.

Получили систему линейных алгебраических уравнений относительно изображений
и
:

Найдем решение системы по формулам Крамера. Вычислим определитель системы
и вспомогательные определители
,
.

Тогда
,
.

Частные решения
и
являются оригиналами для вычисленных изображений. Чтобы найти
, разложим дробь
на сумму простейших:
.

Из этого следует, что

В последнем равенстве положим
. Тогда
, или
. При
:
, значит
. При
:
, откуда
. Следовательно,

Таким образом,
.

Решение линейных дифференциальных уравнений с постоянными коэффициентами и нулевыми начальными условиями с помощью интегралов Дюамеля

Если
- решение уравнения

при нулевых начальных условиях

,
, …,
, (7)

то решением уравнения

при тех же начальных условиях является функция

Доказательство.

Уравнению (6) при нулевых начальных условиях (7) соответствует операторное уравнение

, (10)

где
,- характеристический многочлен уравнения (6).

Уравнению (8) при нулевых начальных условиях (7) соответствует операторное уравнение

(11)

где
, а
.

Из (10) и (11) найдем

Воспользуемся результатами для изображения по Лапласу интегралов Дюамеля

(13)

Положим в формуле (13)
,
и учтем, что
. Тогда получим решение дифференциального уравнения (8) при нулевых начальных условиях в виде

Формула (14) позволяет находить решение линейного дифференциального уравнения с постоянными коэффициентами при нулевых начальных условиях, не находя изображения правой части этого уравнения.

Типовой расчет

1. По данному графику оригинала найти изображение:

Решение. Найдем аналитическое выражение для функции, график которой представлен на рисунке. Прежде всего запишем уравнение прямой, проходящей через точки
и
, и уравнение прямой, проходящей через точки
и
. Как известно, уравнение прямой, проходящей через точки с координатами
и
имеет вид
. В данном случае независимая переменная, поэтому уравнение прямой примет вид
. Подставляя в это уравнение координаты точек А и В получим после упрощения уравнение в виде
, подставляя в уравнение координаты точек В и С, получим после упрощения уравнение в виде
. Тогда функция
имеет вид

(15)

Эту функцию можно записать с помощью функции Хевисайда

(16)

Построим график функции
и убедимся, что он совпадает с исходным заданным графиком

Нужно преобразовать функцию
к такому виду, чтобы аргументы отдельных слагаемых, за исключением постоянных, совпадали с аргументами функций Хевисайда, содержащихся в этих слагаемых. Здесь нужно подвергнуть преобразованию только последнее слагаемое.

Изображение этой функции построим с помощью таблицы, используя теорему запаздывания

(19)

Решим теперь эту задачу с помощью Mathcad. Функция Хевисайда в этом пакете обозначается греческой буквой
, комплексный аргумент изображения обозначается буквой(т.е.
).

Полученный результат совпадает с (17).

2. Найти оригинал по заданному изображению:

Решение. Для решения этой задачи необходимо представить дробь
в виде суммы простейших дробей.

Разложение дроби
на простейшие имеет вид

, (20)

поскольку многочлен
имеет два комплексно сопряженных корня, так как
. Приведем сумму дробей в правой части (20) к общему знаменателю, который совпадает со знаменателем дроби в левой части (20). Тогда получим равенство числителей

Для определения коэффициентов разложения в (20), воспользуемся вначале методом частных значений. Положим в (21)
, тогда получим
.

Для того, чтобы определить коэффициенты
и
, используем метод неопределенных коэффициентов: приравняем коэффициенты при одинаковых степеняхив левой и правой частях равенства (21).

. Отсюда найдем
,
.

Следовательно,
.

Выделим полный квадрат в знаменателе
:

(22).

Теперь с помощью таблицы по заданному изображению можно восстановить

оригинал

Для изображения
с учетом теоремы запаздывания получим из таблицы оригинал

Следовательно,

Приведем решение данной задачи с помощью Mathcad. Для каждого из слагаемых изображения получим оригиналы

Отсюда для исходного изображения оригинал имеет вид

Этот результат совпадает с (23).

3. Найти решение дифференциального уравнения
, удовлетворяющее начальным условиямy(0) = y"(0) = 0.

Для решения данной задачи используем интеграл Дюамеля. Найдем вначале решение
дифференциального уравнения
. Соответствующее операторное уравнение для изображения
имеет вид

или
. Отсюда найдем

. Представим полученную дробь в виде суммы простейших дробей
. Найдем коэффициенты
. Для этого приведем дроби в правой части к общему знаменателю и получим равенство числителей

Для нахождения коэффициентов вначале воспользуемся методом частных значений. Положим
. Тогда получим
. Положим
. Тогда получим
. Для определения значенияприравняем коэффициенты при степенислева и справа в (24):
. Следовательно,
. Следовательно, изображение имеет вид
. По таблице найдем соответствующий оригинал
.. Отсюда

. (25)

В соответствии с формулой (13) решение исходного дифференциального уравнения
представляет собой интеграл

, (26)

- (27)

правая часть исходного уравнения. Отметим, что в (26) использовано свойство симметрии свертки двух функций.

Подставляя (25) и (27) в (26), получим

Следовательно,

. (28)

Приведем решение данной задачи с помощью Mathcad

Обозначим
через
(напомним, что вMathcad комплексная переменная обозначается через)

Найдем оригинал
, затем положим
и найдем производную поот функции

Вычислим
, где
- правая часть исходного уравнения.

Правую часть можно упростить

В результате дальнейшего упрощения получим

Этот результат совпадает с выражением (28), полученным ранее.

Учитывая, что свертка двух функций не зависит от порядка их следования, можно также провести расчет
по формуле (26) в виде

В результате получилось довольно громоздкое выражение. Приведем подобные члены в этом выражении и упростим результат

Этот результат также приводится к виду (28)

4. Операционным методом решить задачу Коши:

(29)

(30)

Решение. Учитывая, что,,

получим операторное уравнение в виде

Отсюда изображение

(31)

Многочлен
имеет корни
,
, поэтомуи выражение для
после упрощения суммы первой и последней дробей преобразуется к виду

(32)

Для того чтобы получить оригинал
для изображения
, нужно дроби, входящие в (32), разложить на простейшие. Найдем это разложение с помощьюMathcad

Операционное исчисление применяется при нахождении как частных, так и общих решений линейных дифференциальных уравнений любого порядка с постоянными коэффициентами, при этом правая часть уравнения на различных интервалах может быть задана различными аналитическими выражениями, а также может иметь точки разрыва. Операционный метод используется для решения однородных и неоднородных систем дифференциальных уравнений, причем правые части неоднородных систем также могут быть заданы на различных интервалах различными аналитическими выражениями и иметь точки разрыва.

Операционное исчисление широко применяется для решения задач электротехники и теории автоматического регулирования, в частности позволяет найти установившийся ток в колебательном контуре при периодическом и непериодическом внешнем напряжении. Операционные методы позволяют рассчитывать процессы в сложных электрических цепях при произвольном внешнем напряжении. Операционные методы позволяют также находить решения уравнений в частных производных, которые появляются в задачах математической физики, например при решении задачи о колебательном движении струн и стержней, о распространении тепла в стержне, плоских пластинах и пространственных телах, о распространении электрических колебаний вдоль длинных цепей.

Операционное исчисление строится на основе преобразования Лапласа.

Преобразованием Лапласа или изображением по Лапласу функции вещественной переменнойназывается функция
комплексной переменной
, определяемая несобственным интегралом

. (1)

Интегралом Лапласа называется интеграл в правой части (1).

Оригиналом называется функция вещественной переменной
, которая удовлетворяет условиям:

1)
при
,

2)
кусочно-непрерывна при
; (2)

3)
при любом, где
некоторые постоянные числа. Числоназывается показателем роста функции
илиабсциссой сходимости интеграла Лапласа.

Функция
может иметь на каждом отрезке при
лишь конечное число точек разрыва первого рода.

Иногда преобразованием Лапласа называется операция перехода от оригинала
к изображению
. Соответствие между
и
записывается в виде
.

Если функция
является оригиналом, то интеграл Лапласа сходится абсолютно и равномерно на комплексной полуплоскости
.

Доказательство. Пусть
, и
. Тогда

Отсюда следует, что интеграл Лапласа сходится абсолютно при
, так как он мажорируется абсолютно сходящимся интегралом. Если же
, то
,где в правой части неравенства получено число. Следовательно, интеграл Лапласа сходится равномерно при
.

Преобразование Лапласа устанавливает связь между оригиналами
и их изображениями. Определенным действиям, производимым над оригиналами соответствуют некоторые действия, производимые над их изображениями, причем действия над изображениями оказываются более простыми, чем над оригиналами. В частности, дифференциальному уравнению относительно оригинала соответствует алгебраическое уравнение относительно изображения. Если решить это алгебраическое уравнение и затем найти оригинал полученного решения, то тем самым будет получено решение исходного дифференциального уравнения.

Единичной функцией Хевисайда называется функция
. График функции Хевисайда имеет вид

Пример 1 . Найти изображение единичной функции Хевисайда.

(3)

Условимся в дальнейшем под функцией
понимать функцию, которая равна нулю при
, т.е.
.

Пример 2. Найти изображение показательной функции
.

для
.

(4)

Пример 3. Найти изображение степенной функции
,
и
,
.

(5)

Во многих задачах математического анализа рассматриваются ситуации, в которых каждая точка одного пространства ставится в соответствие некоторой точке другого (или того же) пространства. Пространства могут быть абстрактными, в которых «точки» в действительности являются функциями. Соответствие между двумя точками устанавливается с помощью преобразования или оператора. В задачу теории операторов входит подробное описание и классификация различных видов преобразований и их свойств, а также разработка символических методов, позволяющих минимизировать и упростить вычисления. Обычно теорию операторов применяют к пространствам, в которых допускается сложение или умножение точек, т.е. линейным пространствам, группам, кольцам, полям и т.д.

Проблемы и приложения.

Пусть D и R – действительные линейные или векторные пространства, необязательно различные. Их элементами являются векторы, поэтому сумма двух элементов и произведение элемента на скаляр определены и удовлетворяют обычным условиям, предъявляемым к векторам. Существование конечных базисов в D и R необязательно. Пусть r , вектор из R , соответствует вектору d из D . Обозначим это соответствие T (d ) = r или Td = r . Тогда T называется оператором с областью определения D и областью значений R . Оператор T является дистрибутивным, если

где λ и λ" – любые действительные числа, а d и d" – любые элементы из D . Если D и R – топологические векторные пространства, в которых λd и d + d" – непрерывные операции, то дистрибутивный непрерывный оператор называется линейным оператором. Если Q содержит D и R , то T 2 (d ) определяется как T (T (d )) и аналогичным образом определяется T n (d ), если все эти операции имеют смысл.

Операционное исчисление позволяет осуществить абстрактные постановки задач и обобщить такие разделы математического анализа, как теория дифференциальных и интегральных уравнений. Мощным стимулом для развития теории операторов стали современные проблемы квантовой теории. Наиболее полные результаты получены для дистрибутивных операторов в т.н. гильбертовом пространстве. Интерес к этой области во многом связан с представлением таких операторов интегральными преобразованиями.

Двумя важными дистрибутивными операторами являются операторы дифференцирования p и интегрирования p –1 . Элементами линейных пространств D и R в этом случае будут функции переменной x . Имеем

где m и n – неотрицательные целые числа. Так как интегрирование приводит к появлению произвольной постоянной, p –1 p необязательно является тождественной операцией p 0 . Формальные правила комбинирования таких операторов восходят к Дж.Булю (1815–1864); например,

В исчислении Хевисайда, разработанном О.Хевисайдом (1850–1925), пространство D ограничено областью определения функций f (x ), тождественно равных нулю при отрицательных x . Главную роль играет функция 1(x ), равная 0 при отрицательных x и 1 при неотрицательных x . Приведем некоторые «правила» исчисления Хевисайда:

Если n ! заменить гамма-функцией Г(n + 1), то первое из правил останется в силе и при нецелых n (определение гамма-функции см . ФУНКЦИЯ).

Основным результатом операционного исчисления принято считать теорему о композиции, или свертке, согласно которой, если F 1 (p )1(x ) = f 1 (x ) и F 2 (p )1(x ) = f 2 (x ), то

Применяя теорему о свертке к p a при a ≠ 0, –1, –2,..., можно определить интегрирование или дифференцирование дробного порядка. Например, рассмотрим выражение

где функция y (x ) и ее первые n – 1 производных обращаются в нуль при x = 0. Пусть y (x ) = Y (p )1(x ), g (x ) = G (p )1(x ). Примем

Предположим, что f (x ) = F (p ) –1 1(x ). Тогда

Стандартные правила включают в себя различные алгоритмы, связанные с разложениями на элементарные дроби рациональных функций асимптотических рядов и т.д. На практике y (x ) = Y (p )1(x ) часто записывают в виде y (x ) ~ Y (p ) или .

К тем же общим результатам приводит и теория функций замкнутого цикла В.Вольтерры (1860–1940). Близкие теории были построены для других операторов, например для x (d /dx ) и для более общих ситуаций с несколькими операциями, Вольтеррой, Пинкерле и др. Для прикладных математиков основное преимущество операционного исчисления Хевисайда заключается в сведении трансцендентных задач с независимой переменной x к алгебраическим задачам для функций, зависящих от p . Чаще всего метод Хевисайда применяется при решении дифференциальных уравнений с постоянными коэффициентами, разностных уравнений и интегральных уравнений с ядром K (x , t ) = K (x – t ). В общем случае при распространении методов операционного исчисления на более сложные уравнения теряется характер «чистой алгебраизации».

Строгое обоснование соотношения F (p )1(x ) = f (x ) было дано с помощью интегральных преобразований Лапласа или Фурье, или абстрактно, в терминах операторов в некоторых линейных топологических пространствах, таких, как гильбертово пространство. Такой подход позволил установить условия применимости эвристических правил.